Sorteringstype met Lucas-sequenties
De relatie tussen tekst en de rest van een pagina is een van de belangrijkste kenmerken van elk ontwerp.
Ritme, nadruk en toon komen allemaal in gevaar zonder correct geschaald type. Het selecteren van tekstformaten is echter vaak een moeizame en frustrerende ervaring, zonder een gestandaardiseerd startpunt om ons te informeren.
Als gevolg hiervan vinden we webdesigners vaak terugvallen op de standaardopties van applicaties - 8pt, 10pt, 12pt, 14pt, 18pt - voor een betere oplossing.
Die betere oplossing is het instellen van lettergroottes niet door individuele grillen, maar volgens een vooraf bepaald systeem; een systeem dat eenvoudig in gebruik is, praktisch te implementeren op het web en vooral flexibel genoeg om ontwerpers een volledig scala aan expressie te bieden. Cue: de Lucas-reeks.
Lucas Sequences
De Fibonacci-reeks - voor het eerst opgenomen in het Westen in de 13e eeuw door Leonardo Fibonacci - is de volgende reeks gehele getallen (hele getallen):
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 ... ad infinitum
De sequentie werd genoemd naar Fibonacci door de eminente 19e eeuwse Franse wiskundige François Édouard Lucas, die een soortgelijke reeks van zijn eigen reeks produceerde, die hij Lucas Numbers noemde:
2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843 ... ad infinitum
De Fibonacci-reeks en Lucas-nummers zijn beide specifieke variaties van de generieke Lucas-reeks.
Lucas-sequenties en integere sequenties in het algemeen zijn het onderwerp geweest van een levensduur van studie voor vele volleerde wiskundigen, dus we gaan het concept als volgt samenvatten:
- Elk gegeven getal in de reeks is de som van de twee voorgaande getallen zoals beschreven in deze formule: n = n-1 + n-2
- De eerste twee nummers in de reeks - ook wel seednummers genoemd - worden willekeurig geselecteerd.
Waarom een Lucas-reeks gebruiken om het type in te stellen?
Lucas-sequenties, in het bijzonder in de vorm van de Fibonacci-reeks, hebben een nauwe relatie met de gulden snede, die in de natuur wordt herhaald in schelpen, spinnenwebben, wolkenformaties en talloze andere natuurlijke wonderen. Er zijn sterke aanwijzingen dat alles dat we visueel aantrekkelijk vinden, te wijten is aan de relatie van dat formulier tot de gulden snede.
Wat nog belangrijker is, Lucas Sequences biedt ons een schaalbaar raamwerk voor het instellen van een type dat zowel sierlijk als ritmisch is.
Het bepalen van ons eerste zaadnummer
Er is veel discussie over de juiste tekstgrootte voor een website. 12px is nog steeds de meest voorkomende, maar het is niet ongebruikelijk om iets van 10px tot 16px te zien. Dit komt grotendeels voort uit een gebrek aan inzicht in wat lettertypemetingen eigenlijk betekenen. Vreemd genoeg is er voor degenen onder ons die gewend zijn aan standaardisatie - of op zijn minst normen voor standaardisatie - geen standaardmaat in het typeontwerp; twee verschillende letterontwerpers, die exact hetzelfde ontwerp tekenen in software voor het maken van lettertypen, tekenen het waarschijnlijk in verschillende formaten. De variatie tussen verschillende lettertypen is, niet verwonderlijk, maar al te vaak.

Het antwoord op waar te beginnen is razend eenvoudig; onze standaard tekstgrootte is 1em, wat betekent dat ons eerste seednummer 1 is.
Er zijn een aantal belangrijke voordelen aan het gebruik van 1em als uitgangspunt: als relatieve meeteenheid is een em goed geschikt voor responsief ontwerp; door ems en veelvouden van ems te gebruiken, kunnen we ons hele schema verkleinen door de lettergrootte te veranderen; eindelijk is het een nette conceptuele fit met onze Lucas-sequentie en zal het ons helpen herinneren aan de precieze integere sequentie als we het ontwerp later opnieuw moeten bekijken.
Er is niets inherent verkeerd aan het gebruik van percentages in plaats van ems, of zelfs pixels of punten, maar de em is meer dan waarschijnlijk de toekomst van webdesign, dus we kunnen er net zo goed aan wennen.
Het bepalen van ons tweede zaadnummer
Er zijn talloze strategieën voor ons open om ons tweede zaadnummer te bepalen. Sommige ontwerpers hebben een specifieke voorkeur en kiezen 1.2em of iets dergelijks. Andere ontwerpers, die genieten van de mystiek van de Gulden Snede, zouden 1.618em graag willen gebruiken.
Een meer praktische oplossing is om het tweede seed-nummer te bepalen aan de hand van de regelhoogte van de hoofdtekst. Omdat de regelhoogte meestal wordt bepaald door de lengte van de lijn en de lengte van de lijn wordt bepaald door een raster, is deze meer geschikt om af te drukken of om niet-reagerend webontwerp te maken. Omdat we naar de toekomst kijken en de toekomst reageert, zal het niet voor ons werken.
Wat overblijft, deels door een proces van eliminatie en deels vanwege zijn geschiktheid, is de x-hoogte van het type. Of meer specifiek, de relatie van de x-hoogte tot de rest van de glyph.
Een kenmerk van goed ontwerp is de herhaling van sleutelelementen, en het doorvoeren van de verhoudingen van het type naar de pagina als geheel is een geweldige kans om zowel het werk van de letterontwerper te erkennen als ons ontwerp te doordrenken met het karakter van een lettertype.
Onze x-hoogte vinden
Om de x-hoogte van uw lettertype te vinden, moeten we iets als Photoshop of Illustrator openen en wat tekst toevoegen die een oplopende tekst bevat (bijv. 'D') en de letter 'x'. Als u een bitmapeditor zoals Photoshop gebruikt, stelt u de tekst zo groot mogelijk in, zodat u een nauwkeurig resultaat krijgt. In deze voorbeelden heb ik het lettertype ingesteld op 500pt om het te meten.
Meet vervolgens de hoogte vanaf de ascenderlijn tot de basislijn en de hoogte vanaf de top van de x tot de basislijn.
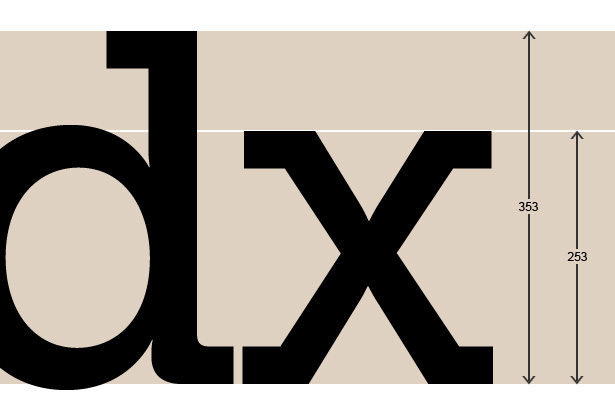
Als je het geluk hebt om toegang te hebben tot goede software voor het ontwerpen van lettertypen, kun je natuurlijk het lettertypebestand openen dat je gaat gebruiken en de x-hoogte en opkijkhoogte uitlezen.
Verdeel nu de x-hoogte door de opklimmende hoogte om de x-hoogte te vinden als een percentage van het geheel:
x-hoogte / ascender-hoogte * 100 = tweede zaadnummer
In het geval van het lettertype in het voorbeeld (Museo Slab) is het resultaat:
253/353 = 0.71671388
of 0,716em
Waarom meten we niet vanaf de top van de ascender naar de onderkant van de afdaler? Omdat tekens niet zowel een ascender als een descender hebben (een occasionele uitzondering is de letter 'f') en bijgevolg zijn de relaties binnen de vormen die het ontwerp van het lettertype omvatten gebaseerd op de relatie tussen de x-hoogte en een langere steel. Het is mogelijk om het daler in plaats daarvan te meten, maar omdat de cap-hoogte (de hoogte van de hoofdletters) meestal erg dicht bij de opklimmende persoon ligt, is dat mijn voorkeur. Als je merkt dat je een lettertype gebruikt met een meer dominante kwaliteit - bijvoorbeeld het contrast in de dikte van verschillende streken - zou je die waarde willen kunnen gebruiken in plaats van de ascender naar x-height ratio.
De bepaling van hoe je bij je tweede zaadnummer komt, is een van de belangrijkste ontwerpbeslissingen die je moet nemen, maar het is niet iets om je zorgen over te maken; kies een nummer uit een hoed als je dat liever hebt, en ga verder, het goede spul moet nog komen.
Het is vermeldenswaard dat als je de vergelijking omdraait en de ascender-hoogte deelt door de x-hoogte, je een getal groter dan één krijgt. In dat geval is je reeks steiler en iets dramatischer.
Onze volgorde maken
Dus we hebben onze twee zaadnummers: 1em en 0.716em en we hebben de formule n = n-1 + n-2:
1 + 0.716 = 1.716
0.716 + 1.716 = 2.432
1.716 + 2.432 = 4.148
enz.
Wat resulteert in de volgende reeks:
1, 0.716, 1.716, 2.432, 4.148, 6.58, 10.728, 17.308, 28.036 ... ad infinitum
Het ontwerpbit
Tot dusverre hebben we ons een weg gebaand door enkele elementaire, maar nuttige wiskunde, en we zijn aangekomen bij een reeks die ons een reeks maten geeft van 1em tot 28.036em en meer als dat nodig is.
We kunnen nu deze waarden sequentieel gebruiken als onze sorteergroottes om een goed geproportioneerd typeschema te maken:

Je zult zien dat we beginnen met p ingesteld op 0.716 en h4 ingesteld op 1, ondanks het feit dat dat niet sequentieel correct is. De reden is dat h4 in termen van hiërarchie belangrijker is dan p. Onze Lucas-reeks moet de hiërarchie op de pagina niet dicteren, het dicteert de schaalrelaties van verschillende elementen. Alleen je inhoud kan hiërarchie dicteren .
Omdat we niet beperkt zijn tot opeenvolgende waarden in onze volgorde en in staat zijn om te kiezen en kiezen welke gehele getallen we gebruiken, bereiken we altijd ritme en structuur met dezelfde reeks. Zelfs als we een zeer dramatische aanpak hanteren:

Precies dezelfde Lucas-reeks kan ook worden gebruikt om een meer gereserveerd, zakelijk schema te maken:

De essentie van dit systeem is dat de schaalrelaties behouden blijven, de hiërarchie evenredig is, maar er is een enorme variëteit beschikbaar voor de ontwerper. Dit is waar u uw geld moet verdienen: door de formaten op de schaal te selecteren om hiërarchie en nadruk te creëren.
Flexibiliteit
Vaak wordt de typegrootte bepaald door meer dan alleen de nadruk: toegankelijkheidsproblemen doen zich voor als we het hebben over een publiek met visuele problemen; de enorme hoeveelheid inhoud kan beperkingen opleggen; we moeten misschien flexibel zijn - letterlijk - bij het ontwerpen van een vloeiende lay-out.
Gelukkig kan CSS deze situatie gemakkelijk aan. Omdat we ems gebruiken voor onze maten, kunnen we ons type instellen met behulp van onze Lucas-reeks en vervolgens het geheel schalen, door een standaardgrootte in te stellen op de body-tag, het ritme van ons ontwerp te behouden, maar de werkelijke waarden te verhogen of te verlagen.

Merk in dit plaatje op dat de p, h2 en h1 maten hetzelfde blijven, allemaal getrokken uit onze reeks. Het is de variatie op de lettertypegrootte van de body-tag (0,8 em aan de linkerkant en 1,4 e aan de rechterkant) die naar beneden loopt, waardoor er radicaal andere resultaten worden verkregen.
Tenslotte
Omdat het afhankelijk is van de onderliggende wiskunde zoals dit systeem is, is het belangrijk om te erkennen dat ontwerp niet kan worden gereduceerd tot een reeks vergelijkingen. Deze methode voor het dimensioneren van het type geeft u een structuur waarmee u kunt werken en helpt u om goed geproportioneerde typeschema's te maken, maar het is aan u als ontwerper om het systeem als een hulpmiddel te gebruiken en niet als een kruk.
De noten en schalen in muziek, zelfs Jazz, kunnen worden teruggebracht tot een reeks vergelijkingen die hun relatie beschrijven, maar er is iemand als John Coltrane voor nodig om die relaties tot leven te brengen.